



Programação de microcontrolador para conversão AD e modulação PWM e projeto de um filtro e conversão DA a partir do PWM.
Este README pode sem baixado em PDF aqui assim como o PDF de uma versão resumida aqui, a versão resumida pode ser vista online aqui
Todos os códigos em .ino com seus respectivos .hex e os arquivos de simulação .simu e imagens de cada passo desde README foram estruturados nas seguintes pastas:
- 1. analogReadSerial
- 2. avaliacaoPWM
- 3. ModulacaoPWM entrada senoidal
- 4. TCCR0B
- 5. ADCSRA
- 6. comFiltroRC
- 7. filtroAtivo
O workspace do filtro projetado no ADS se encontra aqui
Os microcontroladores consistem em um único circuito integrado que apresenta um núcleo de processador, memórias (voláteis e não voláteis) e determinados periféricos de entrada e de saída de informações. Dentre as capacidades do microcontrolador se encontra, devido a presença de um conversor analógico-digital, a possibilidade de converter sinal analógico em digital.
Uma ferramenta extremamente importante, processar e converter informações é essencial, sobretudo quando se verifica a gama de variáveis analógicas e a capacidade de processamento digital dos computadores atuais. Dessa forma, uma seleta parte desse trabalho busca evidenciar essa característica dos microcontroladores.
Ademais, utilizando o ATMega 328, busca-se, através dessa breve pesquisa, explorar a capacidade de gerar um sinal PWM. O PWM (Pulse Width Modulation) ou Modulação de Largura de Pulso é empregado quando se almeja simular um sinal analógico a partir de um sinal digital. Esse mecanismo é possível quando modula-se a largura do pulso de um sinal digital, ou seja, quando se controla quanto tempo a cada período o sinal digital vai ficar em nível alto e por quanto tempo vai permanecer em nível baixo.
Com o objetivo de estudar sobre a conversão A/D, buscou-se, a priori, realizar uma leitura analógica através da função analogRead, por meio da porta analógica A0. Usando como suporte o código a seguir, realizou-se a digitalização da entrada
void setup() {
Serial.begin(9600);
}
void loop() {
int sensorValue = analogRead(A0);
Serial.println(sensorValue);
}
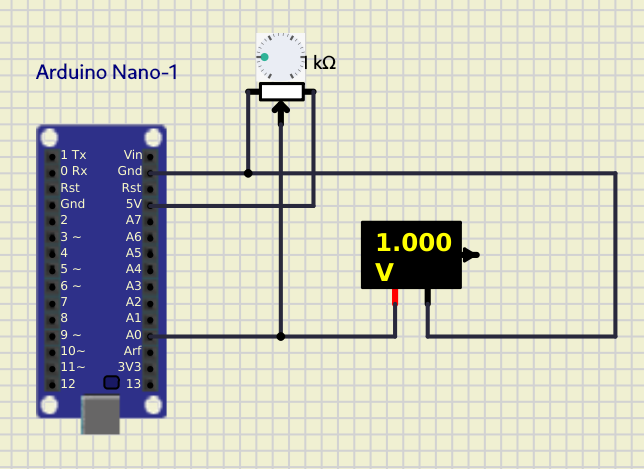
Como mecanismo de alterar a entrada analógica optou-se pela utilização de um potenciômetro que representa uma variável analógica que pode assumir diversos valores. Portanto, ao variar o potenciômetro (0 a 100%), consegue-se realizar uma varredura de 0.5 V. O circuito completo pode ser visualizado na figura 1 a seguir:
| Esquemático do Circuito |
|---|
 |
| Figura 1 – Esquemático para avaliação da conversão AD |
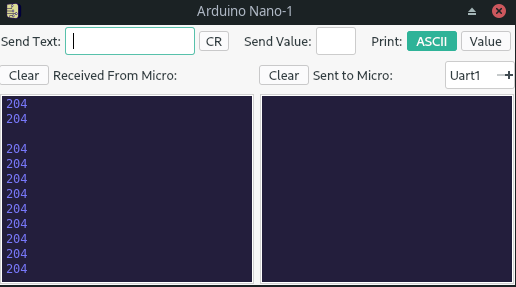
Após realizar o procedimento descrito anteriormente, é imperioso observar o resultado da digitalização da porta serial. Dessa forma, enviou-se o valor decimal da conversão para cada valor correspondente, podendo-se, inclusive realizar um gráfico
| Saída do monitor serial |
|---|
 |
| Figura 2 – Saída serial para entrada de 1.0V |
Após a coleta de dados, montou-se a tabela 1 que correlaciona a entrada e o valor decimal:
| Tensão de entrada |
Valor decimal |
|---|---|
| 0.5 | 102 |
| 1.0 | 204 |
| 1.5 | 306 |
| 2.0 | 408 |
| 2.5 | 511 |
| 3.0 | 613 |
| 3.5 | 715 |
| 4.0 | 818 |
| 4.5 | 920 |
| 5.0 | 1022 |
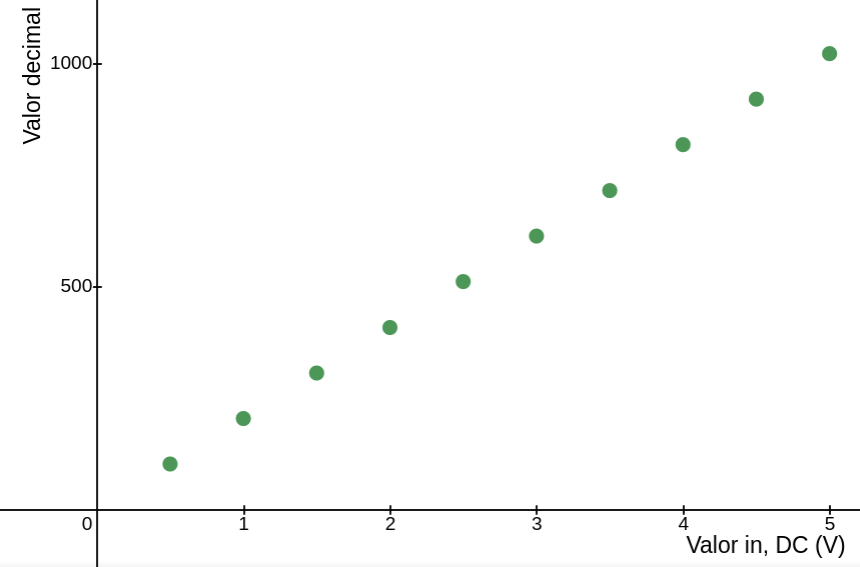
O resultado do gráfico é elucidado na figura a seguir e como se observa, há um comportamento que se assemelha a uma função linear, ou seja, incrementos de tensão de entrada representam o acréscimo proporcional no valor decimal. Contudo, da teoria, observa-se que esse comportamento, se não fosse pela escala preterida de 0.5V, formaria um evidente gráfico digital e discretizado:
| Gráfico |
|---|
 |
| Figura 3 – Gráfico comparativo tensão de entrada e valor serial decimal |
É imperioso entender ainda que, da literatura, sabe-se que a equação que relaciona o valor decimal com o valor de entrada é a equação (1) apresentada abaixo:
Como o arduino apresenta um conversor analógico-digital 10 bits significa que este irá mapear tensões entre 0 e a tensão operacional 5V para valores inteiros entre 0 e 1023. No Arduino UNO, por exemplo, isso permite uma resolução entre leituras de: 5 volts / 1024 unidades, ou 0,0049 volts (4,9 mV) por unidade
O próximo passo do trabalho, após realizar a conversão AD foi, implementar a modulação por largura de pulso (PWM) através da função analogWrite, responsável por acionar uma onda PWM num pino qualquer. Além de gerar um sinal PWM, buscou-se promover uma varredura da variaǘel da razão cíclica 0 a 255 com passo de 51.
Detalhe: A razão de ser de 0 a 255 está relacionada com o fato da quantidade de bits para gerar o PWM ser igual a 8 bits. A seguir verifica-se o código implementado para realizar a avaliação:
void setup() {
pinMode(5,OUTPUT);
}
void loop() {
analogWrite(5, 0); // Segundo parâmetro
// variado (D)
}
Além do código, montou-se o seguinte circuito, elucidado na figura 4, que possibilita realizar a varredura da razão cíclica com um passo de 51:
| Esquemático do circuito para avaliação do PWM |
|---|
 |
| Figura 4 – Esquemático do circuito para avaliação do PWM |
Como se visualiza a seguir, com a varredura da variável que representa a razão cíclica, com D igual a 0, percebe-se que o valor de tensão é permamentente 0 ou nível baixo, enquanto que, conforme aumenta-se a variável da razão cíclica, intensifica também, a porcentagem de tempo em que a variável se encontra com um nível lógico igual a 1, até que se atinja 255 e o nível lógico é permanentemente 1. A figura 5 a seguir demonstra o efeito da varredura:
| D=0 | D=51 | D=102 |
|---|---|---|
 |
 |
 |
| D=153 | D=204 | D=255 |
 |
 |
 |
Para além das observações feitas acima, é fundamental realizar o cálculo do ciclo de tarefa relacionado para cada valor testado acima. Com uma frequência e período definidos, calculou-se o ciclo de tarefa relacionado:
A seguir, na tabela 2, para cada valor testado durante a varredura, determinou-se o ciclo de tarefa relacionado e, como já previsto, aumenta-se o tempo em que a variável se encontra em nível lógico alto, conforme eleva-se a varredura:
| D | ||
|---|---|---|
| 0 | 0 | 0% |
| 51 | 210.9 | 20.67% |
| 102 | 421.9 | 41.36% |
| 153 | 616.6 | 60.45% |
| 204 | 820.7 | 80.46% |
| 255 | 1020.3 | 100.00% |
Para realizar a modulação PWM de uma entrada senoidal, fez-se uso da função analogRead() para digitalizar uma entrada senoidal com características específicas senoidal com f = 10 Hz, Vpp = 5 V e Voffset = 2,5 V. Ademais, utilizou-se também analogWrite() para gerar um sinal PWM por meio da sinal senoidal digitalizado.
O código responsável por exercer essa ação está elucidado a seguir. Para implementar a tarefa fez-se uso da função map, esta última faz com que a leitura analógica da função senoidal (que varia de 0 a 1023) seja recebida pela variável output numa escala de 0 a 255:
void setup() {
pinMode(5,1);
}
void loop() {
int input = analogRead(A0);
int output = map(output, 0, 1023, 0, 255);
analogWrite(5, output);
}
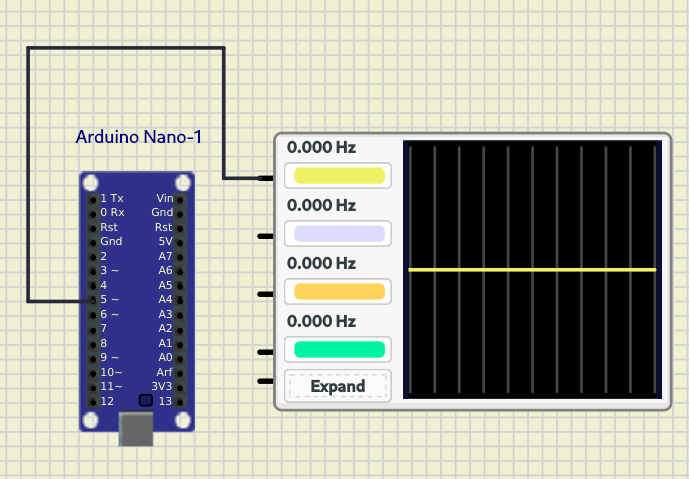
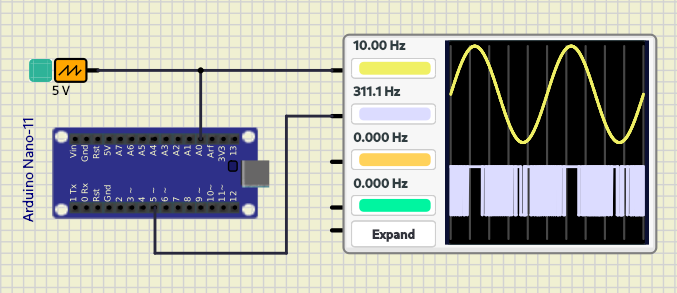
O circuito responsável por realizar a modulação PWM de uma entrada senoidal está elucidado na figura 6 a seguir:
| Esquemático do circuito para modulação PWM |
|---|
 |
| Figura 6 – Esquemático do circuito para modulação PWM de uma entrada senoidal |
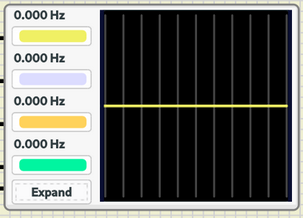
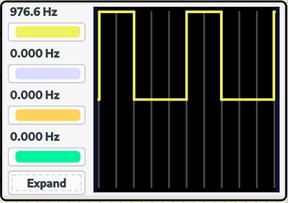
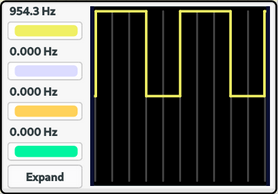
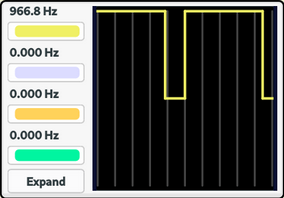
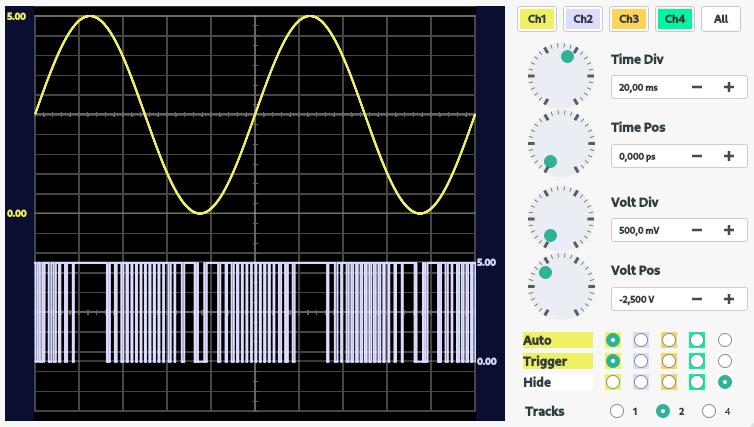
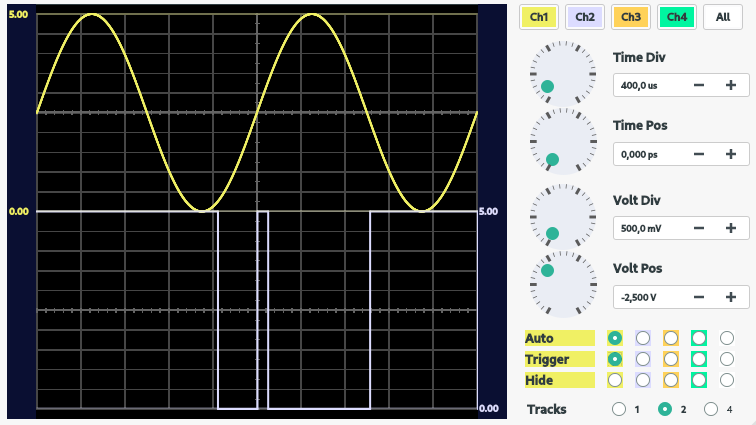
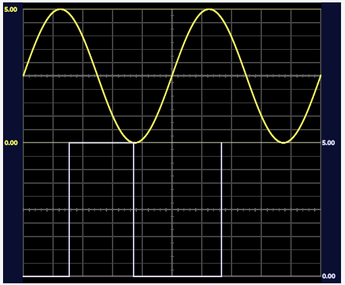
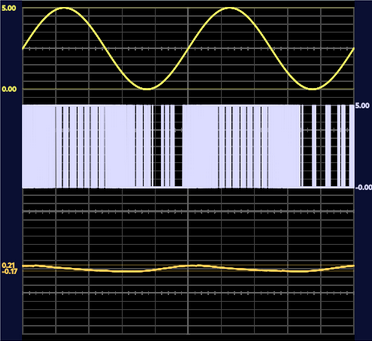
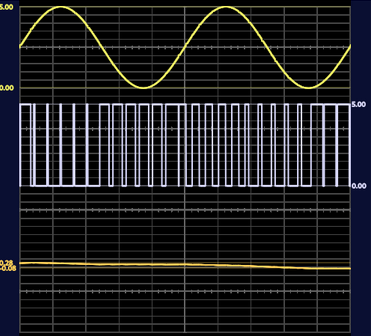
Após a montagem do circuito, variou-se a frequência da onda senoidal, fazendo a assumir = 10 Hz, 100 Hz, 500 Hz e 1 kHz. O resultado pode ser visualizado na figura 7 a seguir:
 |
 |
 |
 |
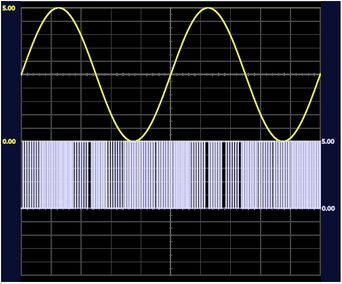
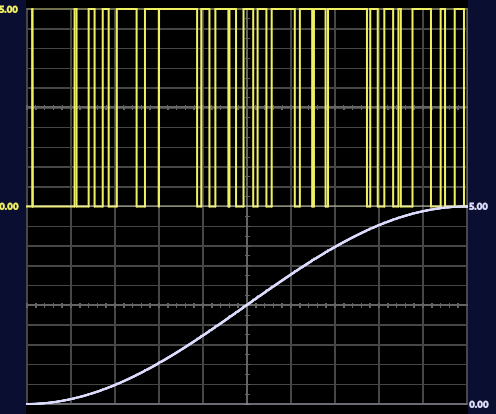
Como se pode observar, a medida que se aumenta a frequência da onda senoidal, o PWM, por conta da quantidade de amostras/tempo, não consegue modular o sinal senoidal de frequências elevadas. Como uma possível solução para o problema, avalia-se o aumento da frequência do PWM. Dessa forma, posterior ao passo descrito, buscou-se analisar os seguintes registradores, almejando-se aumentar a frequência do PWM.
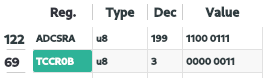
| Análise dos registradores TCCR0B e ADCSRA |
|---|
 |
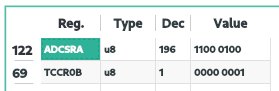
| Figura 8 – Valores dos registradores TCCR0B e ADCSRA do ATMega328P |
Para se reconfigurar os bits do registrador TCC0B para obter a maior frequência possível de PWM primeiramente deve-se consultar o data sheet fornecido pelo fabricante.
| Descrição do registrador TCC0B fornecido pelo fabricante |
|---|
 |
| Figura 9 – Descrição dos bits internos do registrador TCC0B |
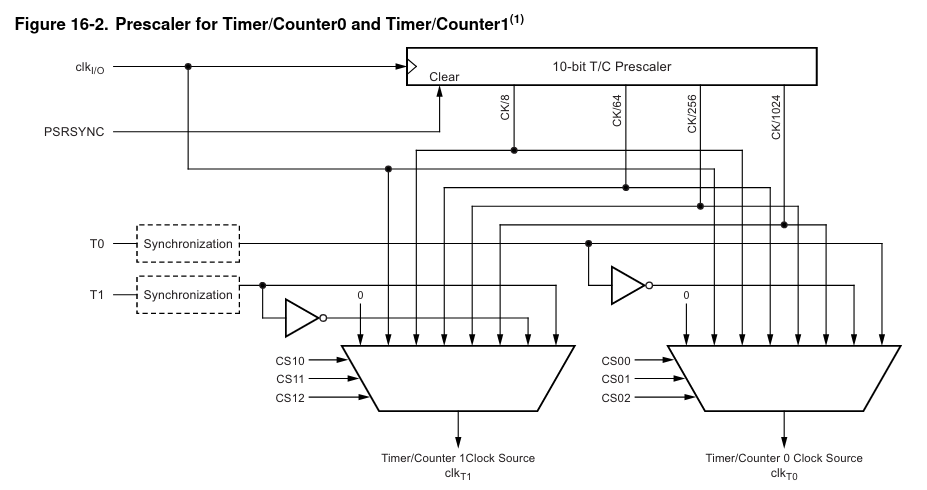
De acordo com a figura 8, sabemos que o valor do registrador TCC0B é de 0b00000011. Analisando especialmente os bits CS02, CS01, CS00, nota-se pela figura 9 e 10 que eles são responsáveis pelo prescaler do clock para o Timer/Counter1, este Timer como sabemos, é utilizado para o circuito do PWM.
| Esquemático do Prescaler |
|---|
 |
| Figura 10 – Funcionamento interno do divisor de frequência |
Analisando também a figura 11, e com o valor do registrador verificado na figura 8, é possível calcular a frequência atual do PWM. Sabendo que a frequência fornecido pelo circuito de cristal externo é de
Esta frequência também foi obtida via simulação, representada na figura 5 e definida na equação (2).
| Divisor de frequência |
|---|
 |
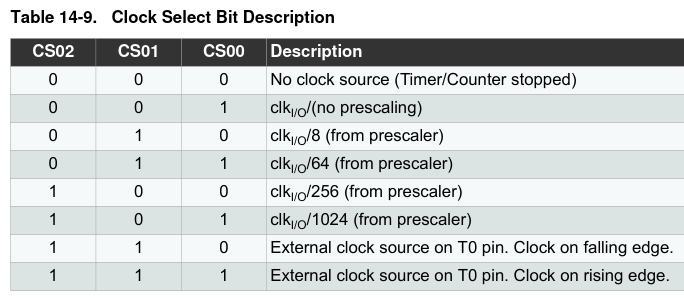
| Figura 11 – Tabela 14.9 do datasheet, configuração dos registradores para prescaler |
Para se obter a maior frequência possível de PWM, deve-se ajustar esses mesmos bits para 0b001, correspondente a opção no prescaling.
Como sabemos o valor atual do registrador, essa operação será realizada a seguir alterando somente os bits necessários, por isso essa configuração (instrução em código) poderia ser diferente se nos deparássemos com um outro microcontrolador em uma situação prática. O código final pode ser visto abaixo:
void setup() {
pinMode(5,1);
TCCR0B&=~(1<<CS01);
}
void loop() {
int input = analogRead(A0);
int output = map(output, 0, 1023, 0, 255);
analogWrite(5, output);
}
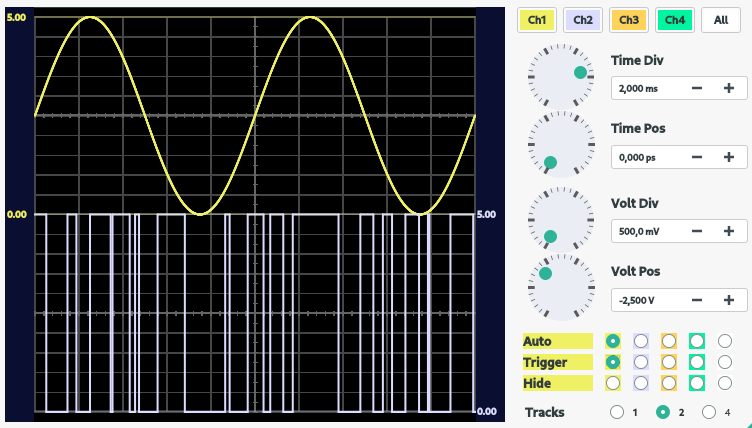
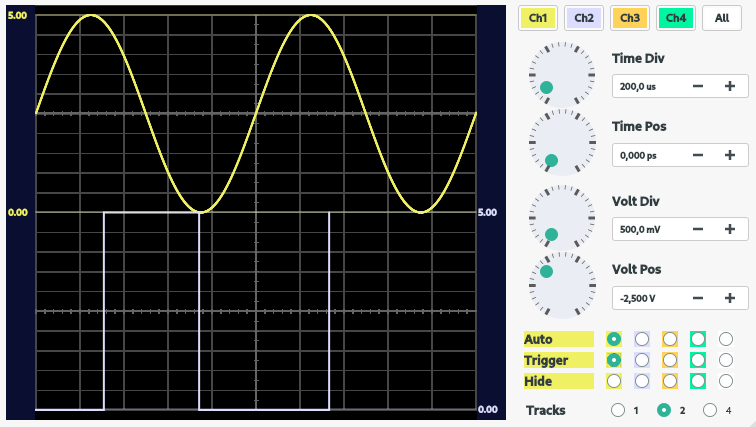
| Resultados anteriores | Resultados após ajuste |
|---|---|
 |
 |
É possível perceber pela figura 12 que o sinal após o ajuste consegue representar melhor a senoide. Esta senoidel utilizada possui frequência
| Análise dos registradores TCCR0B e ADCSRA |
|---|
 |
| Figura 13 – Valores dos registradores TCCR0B e ADCSRA do ATMega328P |
Analisando os registradores, podemos ver a mudança realizada.
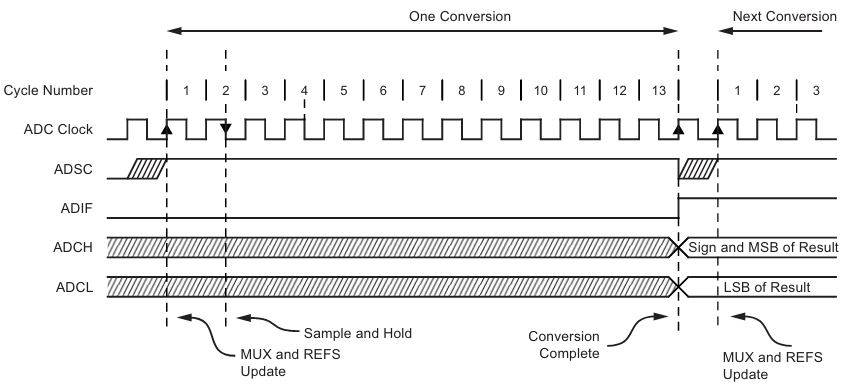
Para definir uma taxa de amostragem, primeiramente, deve-se conhecer o número de ciclos de clock necessários para uma conversão no ADC.
| Diagrama temporal do ADC |
|---|
 |
| Figura 14 – Diagrama temporal do ADC para a obtenção de uma única amostra |
Analisando a figura 14, obtida pelos dados do fabricante, pode-se verificar que são necessários exatos 13 ciclos de clock para uma única amostra. Com isso podemos determinar a frequência do sinal de clock para o circuito do ADC, sabendo a taxa de amostra do ADC desejado de
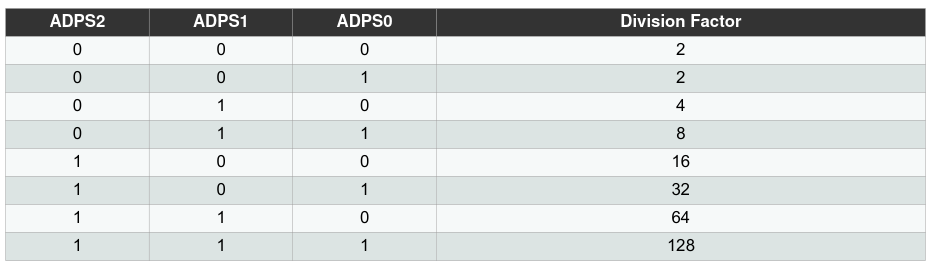
Com o clock do ADC requerido, consultando os dados do fabricante de uma forma análoga à etapa anterior e consultando a figura 15, conclue-se que para obter este clock, deve-se realizar um “prescaler” de 16.
| Bits para prescaler do clock do ADC |
|---|
 |
| Figura 15 – Bits ADSP2, ADSP1, ADSP0 para prescaler do clock do ADC |
Estes bits se encontram nos espaços de memória dos bits menos significativos do registrador ADCSRA.
| Registrador de controle ADCSRA |
|---|
 |
| Figura 16 – Bits ADSP2, ADSP1, ADSP0 como LSB do ADCSRA |
Assim, para obter um fator de divisão de 16, deve-se configurar os bits com os valores 0b100, como é de conhecimento o valor anterior deste registrador, o código para mudar os bits para os desejados (para esta ocasião) está descrito abaixo:
void setup() {
TCCR0B&=~(1<<CS01);
ADCSRA&=~(1<<ADPS1);
ADCSRA&=~(1<<ADPS0);
pinMode(5,1);
}
void loop() {
const int output = map(analogRead(A0), 0, 1023, 0, 255);
analogWrite(5, output);
}
Para se avalizar o resultado, tomamos um intervalo de
| Resultado anterior | Resultado após ajuste em ADCSRA |
|---|---|
 |
 |
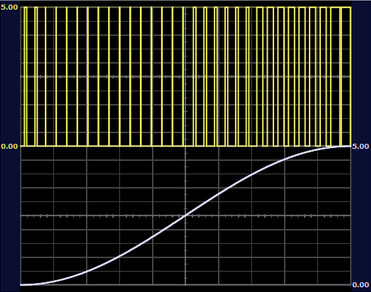
Neste intervalo, foi possível verificar que após o ajuste, obtivemos uma modulação mais suave, não há mudanças tão repentinas nos ciclos de trabalho, isso decorre de uma maior amostragem do sinal.
A partir do presente trabalho foi possível compreender diversas funcionalidades de um microcontrolador, entre elas, a sua capacidade de converter sinais analógicos em digitais com uma precisão de 10 bits, no caso do microcontrolador utilizado.
Além disso, pode-se compreender conceitos importantes como modulação por largura de pulso (PWM) de um sinal senoidal e a possibilidade de alterar registradores de um microcontrolador com o objetivo de aumentar a frequência do PWM e a taxa de amostragem.
Sabe-se que os diferentes sinais podem ser escritos como cossenos e senos ou ainda, por suas somas, que se diferenciam com relação a fase, amplitude e frequência. Em aplicações de Engenharia Elétrica são incontáveis as situações em que se almeja realizar uma alteração na amplitudes relativas de algumas frequências, ou mesmo eliminar determinadas faixas de frequência, a esse processo denominamos o nome de filtragem. Os filtros são os responsáveis por realizar a operação de atenuação ou eliminar uma determinada faixa, enquanto permite a passagem de componentes com outras faixas de frequência. Entre as aplicações, pode-se citar: recortar uma faixa de frequência para que se observe o comportamento de um determinado sistema, ou ainda, melhorar a resposta de um determinado sistema após a retirada de componentes específicos de frequência.
Por meio do teorema da amostragem um sinal de tempo contínuo pode ser completamente representado por suas amostras uniformemente espaçadas no tempo, em um período T , isto é, a informação contida no sinal em tempo contínuo amostrado é equivalente ao do sinal discreto e de forma a minimizar ou eliminar o erro atrelado a essa operação, deve-se manter uma alta taxa de amostragem para a aplicação em questão. Entre as aplicações, pode-se citar a gravação de um áudio de voz por um celular, é óbvio que o sinal de áudio não está em tempo contínuo, contudo a taxa de amostragem está suficientemente alta ao ponto dos erros não serem percebidos pelo ouvido humano.
Dessa forma, após compreender sobre filtros e conversão analógica digital (AD), a presente etapa do trabalho busca realizar o projeto de dois filtros de ordens diferentes para promover conversão D/A a partir de um sinal PWM.
O procedimento inicial para o trabalho foi o estudo, estruturação e desenvolvimento dos dois filtros solicitados conforme os requisitos a seguir:
- Arquiteturas: filtros RC passivo e RC-Ativo
- Seletividade: passa-baixas e passa banda
- Frequência central (de corte):
$f_0 = 1 kHz$ - RC-Ativo:
$N = 2$ ,$K_{\omega_0} = 1$ ,$Q = 10$ .
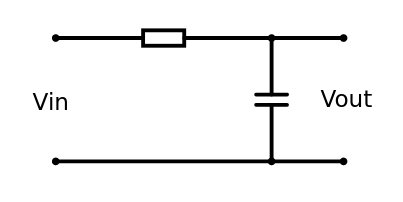
O primeiro filtro implementado foi o de primeira ordem, também conhecido como filtro RC (Resistor – Capacitor) passivo, com frequência central de 1kHz. A seguir vê-se o procedimento realizado para o dimensionamento dos componentes:
Assumindo
Por fim verifica-se na figura 18 a topologia e os valores dos componentes assumidos para montar esse circuito.
Para o projeto do filtro passa faixa de segunda ordem, utilizamos a equação de transferência:
De posse das espeficicações apresentadas, pode-se determinar os coeficientes numéricos da função de transferência do filtro.
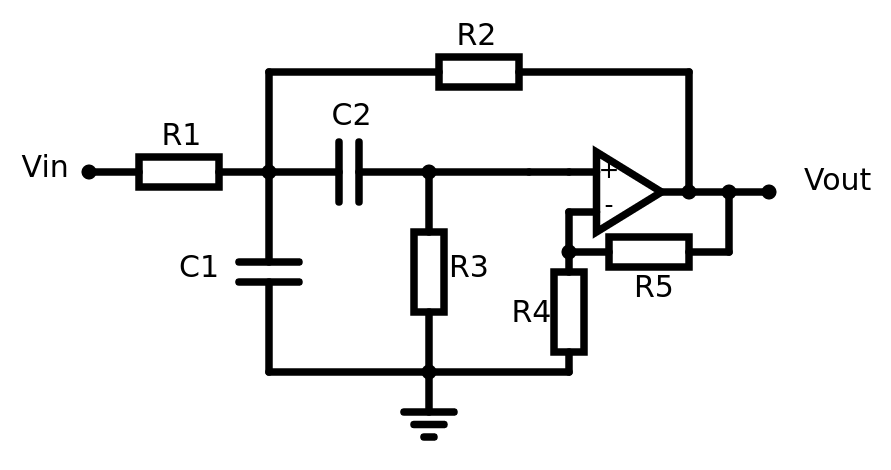
A topologia utilizada para implementação deste filtro será a Sallen-&-Key.
A função de transferência deste filtro está representada abaixo:
Analisando a equação de transferência, podemos implementar o filtro conforme a equação 7, assim temos:
Fazendo
Como na função transferência, o valor de R aparece sempre em par com C, podemos aumentar um, na mesma proporção de diminuição de outro valor mantendo o produto
Utilizando o mesmo valor de capacitor do filtro passivo
E assim, para determinar o
E com o valor de k, podemos atribuir um valor para
De posse desses valores, podemos determinar o ganho para frequencia zero.
Por isso utilizamos resistores em divisor de tensão na entrada para diminuir o ganho por este mesmo fator:
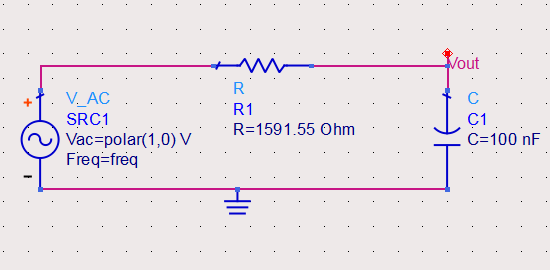
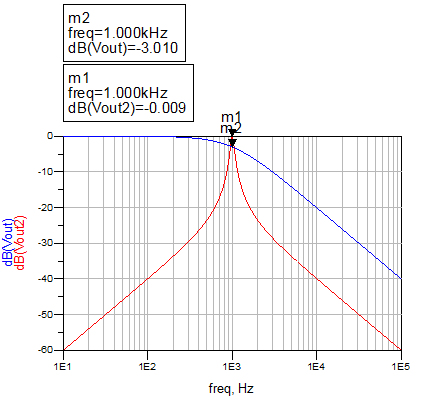
O resultado do filtro passa baixa implementado analiticamente pode ser observado a seguir na figura 19:
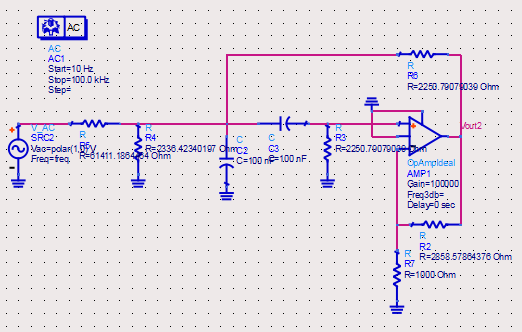
Na figura 20, a seguir, é possível também, verificar a topologia do filtro passa faixa, sem, contudo, realizar a alteração promovida para definir um K máx igual a 1:
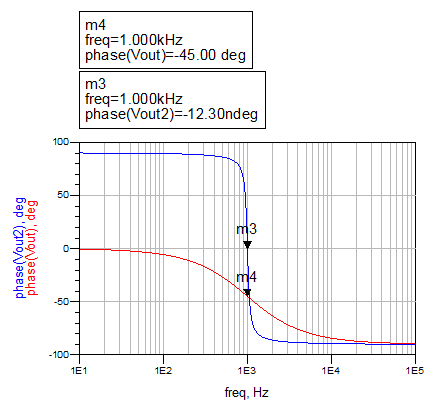
Nas figura 21 e 22 abaixo pode-se comparar o comportamento dos dois filtros, o de primeira ordem com o seu comportamento característico e o passa faixa centralizado em 1KHz.
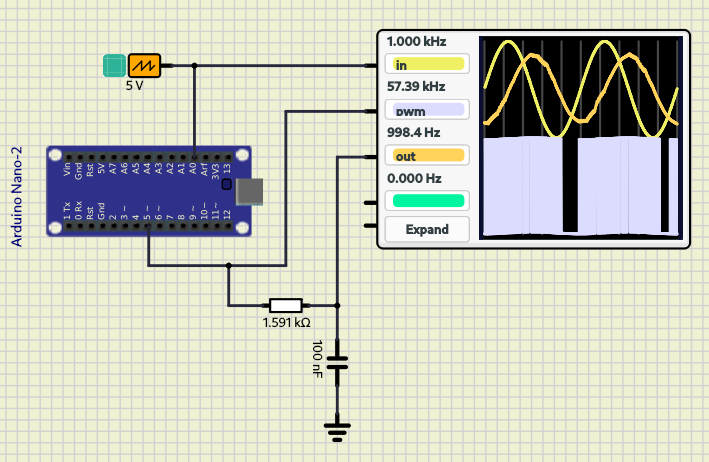
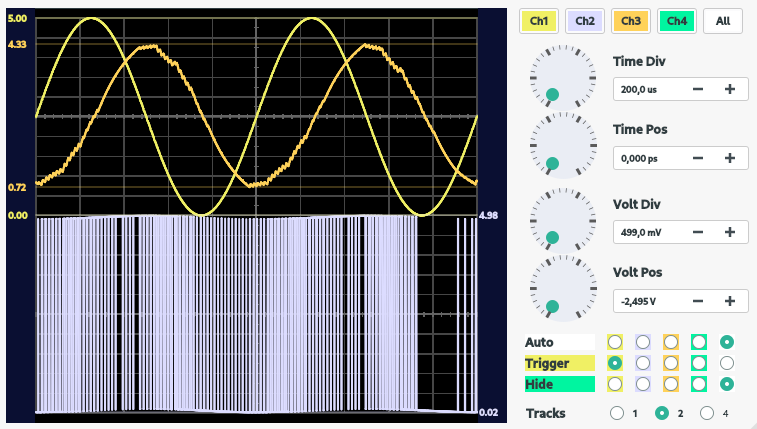
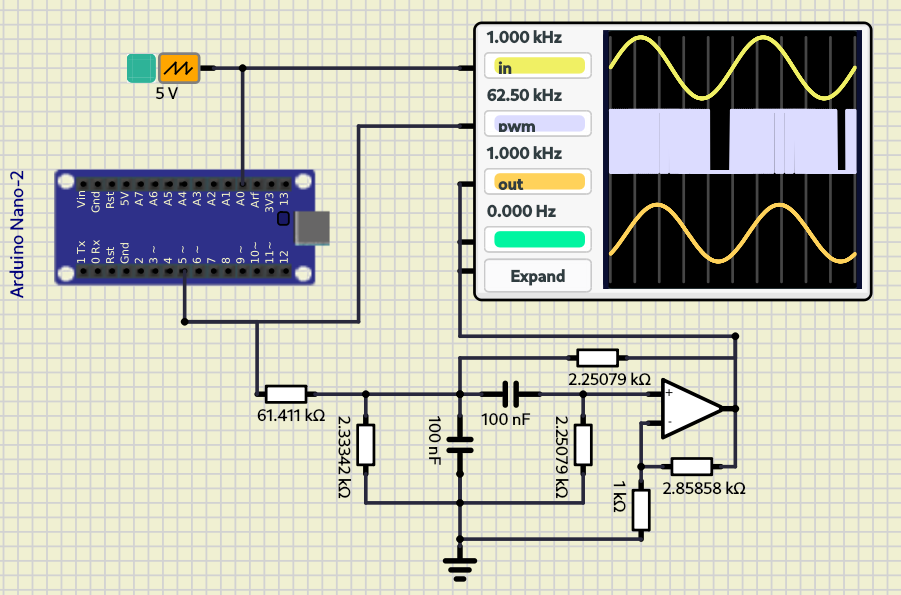
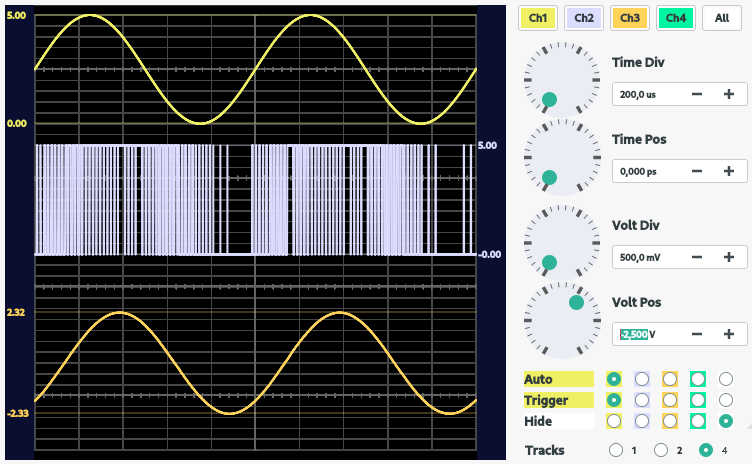
O resultado da implementação do filtro RC dimensionado no ADS em conexão com o osciloscópio pode ser visualizado a seguir:
O que se observa é a reconstrução do sinal senoidal por meio da atuação do filtro no sinal PWM PWM. Verifica-se ainda, como um comportamento inerente do filtro RC, um defasamento de 45° entre saída e entrada.
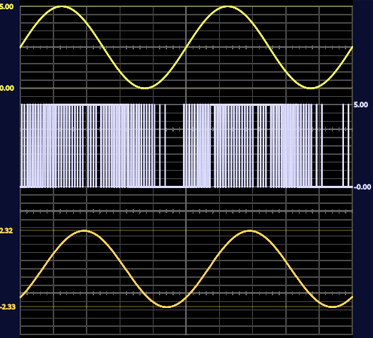
O resultado da implementação do filtro RC dimensionado no ADS em conexão com o osciloscópio pode ser visualizado a seguir:
O resultado da atuação do circuito ativo é a satisfatória reconstrução do sinal senoidal com frequência 1kHz, sem, contudo, provocar uma defasagem entre os sinais.
 |
 |
 |
Na figura 27, pode-se analisar a atuação do filtro passa faixa, atenuando o sinal para componentes do sinal que se encontram fora da faixa de frequência para o qual o filtro foi projetado.
Através da pesquisa pode-se compreender a atuação de dois tipos de filtros diferentes: o passa baixa RC e o filtro ativo passa faixa de segunda ordem. Como descrito anteriormente, o filtro passa baixa causou uma defasagem de 45° no sinal de saída com relação ao sinal de entrada PWM, por outro lado, o filtro RC ativo não causa defasagem entre a saída e a entrada.
Por fim, pode-se concluir, não somente a importância dos filtros, mas também a capacidade de se utilizá-los em conjunto com microcontroladores para filtrar sinais e auxiliar na obtenção de dados desejados.
Noceti-Filho, Sidnei, “Filtros Seletores de Sinais,” Editora da UFSC, Florianópolis, 2003.
Arduino Language Reference https://www.arduino.cc/reference/en/.
LATHI, B. P. Sinais e Sistemas Lineares. 2ª Ed., Porto Alegre, Editora Bookman, 2006. 856p.











Leave a Reply